Standard deviations can be obtained from standard errors, confidence intervals, t values or P values that relate to the differences between means in two groups. The difference in means itself (MD) is required in the calculations from the t value or the P value. An assumption that the standard deviations of outcome measurements are the same in both groups is required in all cases, and the standard deviation would then be used for both intervention groups. We describe first how a t value can be obtained from a P value, then how a standard error can be obtained from a t value or a confidence interval, and finally how a standard deviation is obtained from the standard error. Review authors may select the appropriate steps in this process according to what results are available to them. Related methods can be used to derive standard deviations from certain F statistics, since taking the square root of an F value may produce the same t value. Care is often required to ensure that an appropriate F value is used, and advice of a knowledgeable statistician is recommended.
Where actual P values obtained from t-tests are quoted, the corresponding t value may be obtained from a table of the t distribution. The degrees of freedom are given by NE + NC – 2, where NE and NC are the sample sizes in the experimental and control groups. We will illustrate with an example. Consider a trial of an experimental intervention (NE = 25) versus a control intervention (NC = 22), where the difference in means was MD = 3.8. It is noted that the P value for the comparison was P = 0.008, obtained using a two-sample t-test.
The t value that corresponds with a P value of 0.008 and 25+22–2=45 degrees of freedom is t = 2.78. This can be obtained from a table of the t distribution with 45 degrees of freedom or a computer (for example, by entering =tinv(0.008, 45) into any cell in a Microsoft Excel spreadsheet).
Difficulties are encountered when levels of significance are reported (such as P<0.05 or even P=NS which usually implies P>0.05) rather than exact P values. A conservative approach would be to take the P value at the upper limit (e.g. for P<0.05 take P=0.05, for P<0.01 take P=0.01 and for P<0.001 take P=0.001). However, this is not a solution for results which are reported as P=NS: see Section 7.7.3.7.
The t value is the ratio of the difference in means to the standard error of the difference in means. The standard error of the difference in means can therefore be obtained by dividing the difference in means (MD) by the t value:
![]() .
.
In the example, the standard error of the difference in means is obtained by dividing 3.8 by 2.78, which gives 1.37.
If a 95% confidence interval is available for the difference in means, then the same standard error can be calculated as:
![]()
as long as the trial is large. For 90% confidence intervals 3.92 should be replaced by 3.29, and for 99% confidence intervals it should be replaced by 5.15. If the sample size is small then confidence intervals should have been calculated using a t distribution. The numbers 3.92, 3.29 and 5.15 need to be replaced with larger numbers specific to both the t distribution and the sample size, and can be obtained from tables of the t distribution with degrees of freedom equal to NE + NC – 2, where NE and NC are the sample sizes in the two groups. Relevant details of the t distribution are available as appendices of many statistical textbooks, or using standard computer spreadsheet packages. For example, the t value for a 95% confidence interval from a comparison of a sample size of 25 with a sample size of 22 can be obtained by typing =tinv(1-0.95,25+22-2) in a cell in a Microsoft Excel spreadsheet.
The within-group standard deviation can be obtained from the standard error of the difference in means using the following formula:
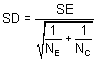
In the example,
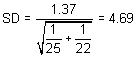 .
.
Note that this standard deviation is the average of the standard deviations of the experimental and control arms, and should be entered into RevMan twice (once for each intervention group).