This is an archived version of the Handbook. For the current version, please go to training.cochrane.org/handbook/current or search for this chapter here.

16.4.6.4  Example

As an example, suppose a cross-over trial reports the following data:

 

Intervention E

(sample size 10)

ME = 7.0,

SDE = 2.38

Intervention C

(sample size 10)

MC = 6.5,

SDC = 2.21

 

Mean difference, imputing SD of differences (SDdiff)

The estimate of the mean difference is MD = 7.0 – 6.5 = 0.5. Suppose that a typical standard deviation of differences had been observed from other trials to be 2. Then we can estimate the standard error of MD as

.

The numbers 0.5 and 0.632 may be entered into RevMan as the estimate and standard error of a mean difference, under a generic inverse variance-outcome.

 

Mean difference, imputing correlation coefficient (Corr)

The estimate of the mean difference is again MD = 0.5. Suppose that a correlation coefficient of 0.68 has been imputed. Then we can impute the standard deviation of the differences as:

 

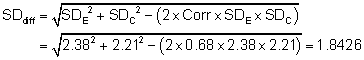
The standard error of MD is then

 .

The numbers 0.5 and 0.583 may be entered into RevMan as the estimate and standard error of a mean difference, under a generic inverse-variance outcome. Correlation coefficients other than 0.68 should be used as part of a sensitivity analysis.

 

Standardized mean difference, imputing correlation coefficient (Corr)

The standardized mean difference can be estimated directly from the data:

.

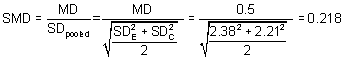
The standard error is obtained thus:

 .

The numbers 0.218 and 0.256 may be entered into RevMan as the estimate and standard error of a standardized mean difference, under a generic inverse-variance outcome.

 

We could also have obtained the SMD from the MD and its standard error:

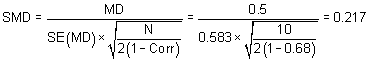
The minor discrepancy arises due to the slightly different ways in which the two formulae calculate a pooled standard deviation for the standardizing.